A999999's Blog

菜狗的第二场 Div.1，感觉晚上临时开窍了，能上橙名。

场上做出了 A ~ C，同时 D 的解法已经想出来了，碍于码力没有写完。

后续的题稍微看下，不一定会 / 能补了。

本文讨论 CCPC Final 2023 J 的与官方解法（from Lynkcat）略有区别的线性解法。

题目传送门：CCPC Final 2023 J

题解视频传送门：第九届 CCPC 总决赛题解

目前进度：

目前进度：

目前进度：

目前进度：

目前进度：

\(2019.6.29\ update:\)给出了时间复杂度的证明，更新了\(L_AT^EX\)

先引入一个问题：

1
2

给定一颗有n个节点的树，给定根节点
每次给出点对(x,y)，查询x到y路径上深度最小的节点(即LCA)。

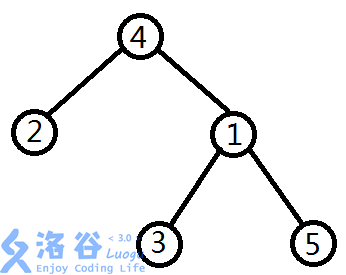
看到这样的题目，大家首先想到的是暴力吧？

1. 从\(x\)出发向上走到根，标记每个经过的节点。

2. 从\(y\)出发向上走，经过的第一个有标记的节点就是"x到y路径上深度最小的节点"\((LCA)\)。

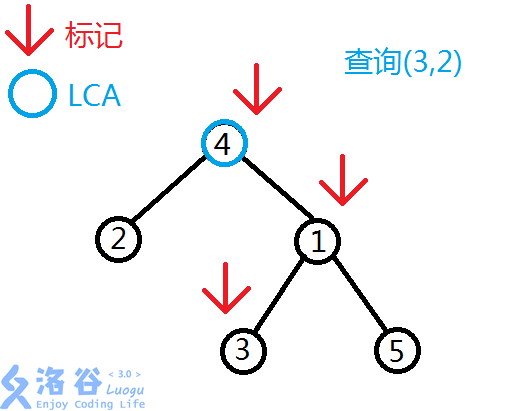
\(Code:\)

1
2
3
4
5
6
7
8
9

int LCA(int x,int y)
{
    if(x==y)return x;
    while(x!=root)vis[x]=true,x=fa[x];
    while(y!=root)
        if(vis[y])return y;
        else y=fa[y];
    return root;
}

但是让我们算算复杂度... \(\Theta(N)\ \)TLE

为什么复杂度如此之高？明显是因为走得太慢了。

我们需要更好的算法。

怎么做呢？

睿智的先人想到了倍增树剖

先把树剖分成一条条的链

每次直接跳一整条链，不就快了吗？

于是，树链剖分(\(Tree-chain\ Partition\))诞生了。