重链剖分

发表于 更新于 分类于 阅读次数： 本文字数： 4.8k 阅读时长 ≈ 18 分钟

\(2019.6.29\ update:\)给出了时间复杂度的证明，更新了\(L_AT^EX\)

先引入一个问题：

1
2
给定一颗有n个节点的树，给定根节点
每次给出点对(x,y)，查询x到y路径上深度最小的节点(即LCA)。
树

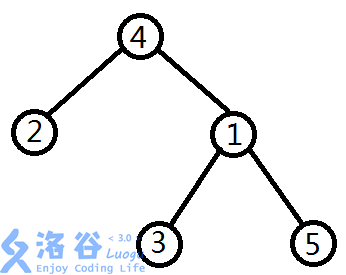
看到这样的题目，大家首先想到的是暴力吧？

  1. 从\(x\)出发向上走到根，标记每个经过的节点。

  2. 从\(y\)出发向上走，经过的第一个有标记的节点就是"x到y路径上深度最小的节点"\((LCA)\)。

(3,2)

\(Code:\)

1
2
3
4
5
6
7
8
9
int LCA(int x,int y)
{
    if(x==y)return x;
    while(x!=root)vis[x]=true,x=fa[x];
    while(y!=root)
        if(vis[y])return y;
        else y=fa[y];
    return root;
}

但是让我们算算复杂度... \(\Theta(N)\ \)TLE

为什么复杂度如此之高？明显是因为走得太慢了。

我们需要更好的算法。

怎么做呢？

睿智的先人想到了倍增树剖

先把树剖分成一条条的链

每次直接跳一整条链，不就快了吗？

于是，树链剖分(\(Tree-chain\ Partition\))诞生了。

预处理

先来说剖分：

剖分，是指依据某种运算，将几个节点分入同一条链，而将一颗树分成几条链的方法。

看不懂没关系反正它不重要

常见的剖分有三种： 1. 重链剖分 2. 实链剖分（Link-Cut Tree才用） 3. 长链剖分（几乎不用）

所以，我们讲的是重链剖分

重链剖分依据啥呢？依据的是儿子的子树大小，即\(x\)子树最大的儿子与\(x\)属于同一条重链。

首先定义几种变量： - \(dep_x\)：\(x\)的深度 - \(fa_x\)：\(x\)的父亲 - \(siz_x\)：以\(x\)为根的子树的节点数 - \(son_x\):\(x\)的重儿子 - \(top_x\):\(x\)所在重链的顶端编号 - \(root\):整棵树的根 - \(son(x)\):\(x\)的儿子所构成的集合

所以我们先要dfs一遍把前4种值算出来。

\(Code:\)

(\(head,ver,next\)均为邻接表,不会的你还看什么树剖请先学会)

1
2
3
4
5
6
7
8
9
10
11
12
void dfs1(ci&x){//ci -> const int,后文同
    siz[x]=1;
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x])continue;
        fa[y]=x;dep[y]=dep[x]+1;dfs1(y);
        if(siz[son[x]]<siz[y])son[x]=y;//求重儿子
        siz[x]+=siz[y];
    }
}
//以下语句加在main(int argc,char **argv)/main() 中
dep[root]=1;dfs1(root);

算完了前\(4\)种值，\(top\)该怎么算呢？

根据定义，一条重链上的节点的\(top\)值相同。

而在重链剖分中，\(x\)和\(son_x\)在一条重链上。

是不是发现了什么

于是我们得到了一条规律： \[ top_x= \begin{cases} &x &|x\neq son_{fa_x}\\ &top_{fa_x} &|x=son_{fa_x} \end{cases} \]

是不是很简单

所以我们就可以愉快的再dfs一遍计算啦

\(Code:\)

1
2
3
4
5
6
7
8
9
10
11
void dfs2(ci&x){
    if(!son[x])return;
    top[son[x]]=top[x];dfs2(son[x]);//直接在fa[x]处赋值，减少参数传递
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x]||y==son[x])continue;
        top[y]=y;dfs2(y);//非重儿子的top[]一定是自己
    }
}
//以下语句加在main(int argc,char **argv)/main() 中
top[root]=root;dfs2(root);

预处理复杂度\(\Theta(N)\)

剖完后的树 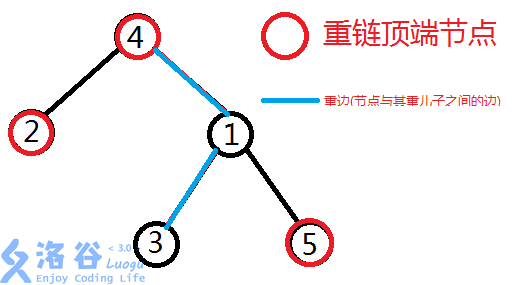例重链

查找LCA

有人问，把链剖出来有对于查LCA什么用呢？

我答：还记得暴力为什么TLE吗？

走太慢啦！

所以，树链剖分的实际作用——加速！

但是，剖完后如何查找呢？

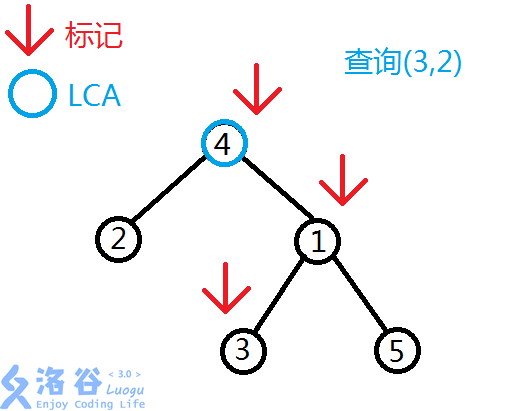
经过苦思冥想， 我们发现一条规律：

无论什么时候，只要两个节点不在一条重链上\((\)即\(top_x!=top_y)\)，那么他们的\(LCA\)肯定不在深度大的那条重链上。

所以，我们可以这样： 1. 对于点对\((x,y)\)，记\(fx=top_x,fy=top_y\). 2. 如果\(fx!=fy\)，转第3步；否则转第4步. 3. 将\(fx,fy\)中\(dep[]\)值大的往上跳(设\(dep_{fx}>dep_{fy}\))，更新\(((x,y)->(fa_{fx},y))\)，回到第2步. 4. 这时\((x,y)\)肯定在一条重链上\((top_x=top_y)\)，而深度较小的那个就是\(LCA\).

\(Code:\)

1
2
3
4
5
6
7
8
9
10
int LCA(int x,int y)
{
    int fx=top[x],fy=top[y];
    while(fx!=fy)
    {
        if(dep[fx]<dep[fy])std::swap(x,y),std::swap(fx,fy);
        x=fa[fx],fx=top[x];
    }
    return dep[x]<dep[y]?x:y;
}

那么这种加速跳法的效果怎么样呢？

可以证明单次操作的时间复杂度 \(\Theta(lgN)\)。

证明

我们需要\(3\)个定理：

  1. \(\forall y\in son(x)\ \&\ y\neq son_x\)，都有\(siz_y\le \frac{siz_x}{2}\)

反证法，假设有 \(siz_y>\frac{siz_x}{2}\)且\(y\in son(x)\) 那么就有 \(y=son_x\)，与定理矛盾 所以假设不成立，原命题成立

  1. \(\forall x\in son(root)\) ,从 \(root\) 到 \(x\) 的路径上存在不超过 \(lgN\) 条轻边

因为每经过一条轻边，到达的点的\(siz\)就会减半 所以最多减 \(lgN\) 次 \(siz_x\) 就变成 \(1\) 了（到达叶子节点）

  1. \(\forall x\in son(root)\) ，从 \(root\) 到 \(x\) 的路径上存在不超过 \(lgN\) 条重链

因为一条重链的两端必定是轻边 所以重链的数量比轻边少一条（重链通向 \(root\) 除外） 最坏情况下轻重链数量一样，为 \(lgN\)

如果每次我们跳过一条重链，这样的重链有 \(lgN\) 条

时间复杂度就为 \(\Theta(lgN)\) 啦

例题P3379

找\(LCA\)的板子题

Code(DFS)

 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<algorithm>
#include<cstdio>
#define N 500010
#define M 500010
#define ci const int
using namespace std;
int head[N],ver[M<<1],next[M<<1],tot;
int dep[N],fa[N],siz[N],son[N],top[N];
int n,m,root;
void add(ci&x,ci&y){ver[++tot]=y;next[tot]=head[x];head[x]=tot;}
void dfs1(ci&x)
{
    siz[x]=1;
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x])continue;
        fa[y]=x;dep[y]=dep[x]+1;dfs1(y);
        if(siz[son[x]]<siz[y])son[x]=y;
        siz[x]+=siz[y];
    }
}
void dfs2(ci&x)
{
    if(!son[x])return;
    top[son[x]]=top[x];dfs2(son[x]);
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x]||y==son[x])continue;
        top[y]=y;dfs2(y);
    }
}
int LCA(int x,int y)
{
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        x=fa[top[x]];
    }
    return dep[x]<dep[y]?x:y;
}
signed main(int argc,char **agrv)
{
    scanf("%d%d%d",&n,&m,&root);
    for(int i=1,x,y;i<n;++i)
        scanf("%d%d",&x,&y),add(x,y),add(y,x);//记得添双向边哦
    dep[root]=1;dfs1(root);
    top[root]=root;dfs2(root);
    register int x,y;
    while(m--)
        scanf("%d%d",&x,&y),printf("%d\n",LCA(x,y));
    return 0;
}

这里是BFS实现版（不知道为什么更慢）

Code(BFS)

 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<algorithm>
#include<cstdio>
#define N 500010
#define ci const int
using std::swap;
int head[N],ver[N<<1],next[N<<1],tot;
int dep[N],fa[N],son[N],siz[N],top[N];
int q[N],sta[N],seg[N],rev[N];
int n,m,root;
void add(ci&x,ci&y){ver[++tot]=y;next[tot]=head[x];head[x]=tot;}
void bfs()
{
    int l=0,r=1,x;
    dep[q[1]=root]=1;
    while(l!=r)
    {
        x=q[++l];
        for(int k=head[x],y;y=ver[k],k;k=next[k])
        if(!dep[y])
            q[++r]=y,fa[y]=x,dep[y]=dep[x]+1;
    }
    for(int i=r;x=q[i],i;--i)
        ++siz[x],siz[fa[x]]+=siz[x];
    siz[0]=0;
    for(int i=1;x=q[i],i<=r;++i)
    {
        if(!top[x])top[x]=x;
        for(int k=head[x],y;y=ver[k],k;k=next[k])
        if(y!=fa[x]&&siz[son[x]]<siz[y])
            son[x]=y;
        if(son[x])top[son[x]]=top[x];
    }
    for(int i=r,tp,p;x=q[i],i;--i)
        if(siz[x]==1)
        {
            for(p=x,tp=0;top[p]==top[x];p=fa[p])
                sta[++tp]=p;
            for(;tp;--tp)
                seg[sta[tp]]=++seg[0],rev[seg[0]]=sta[tp];
        }
}
int LCA(int x,int y)
{
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        x=fa[top[x]];
    }
    return dep[x]<dep[y]?x:y;
}
signed main(int argc,char **argv)
{
    scanf("%d%d%d",&n,&m,&root);
    for(int i=1,x,y;i<n;++i)
        scanf("%d%d",&x,&y),add(x,y),add(y,x);
    bfs();
    register int x,y;
    while(m--)
        scanf("%d%d",&x,&y),printf("%d\n",LCA(x,y));
    return 0;
}

套线段树

又有睿智聪明的小盆友问了：

这个奇怪的东西怎么套线段树呢？

我们来再看一看树链剖分后轻重边的分配情况：

如果我们把链拼成一个序列，就像这样：

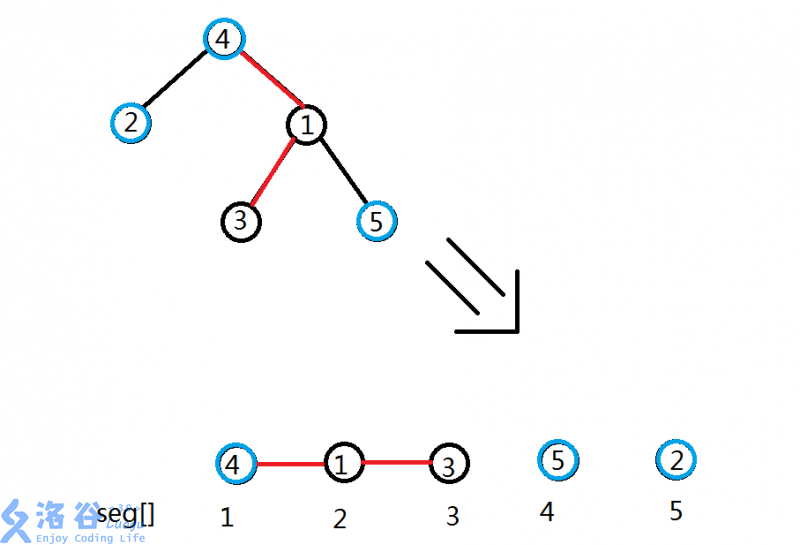
那么是不是可以用线段树维护呢？

不是也得是

如何确定每个节点在序列中的位置呢？

我们回到\(dfs2()\)中

很容易发现一个性质：

对于同一条重链上的节点，他们一定是被连续访问的！

所以我们可以直接在\(dfs2()\)中计算出每个节点在序列中的位置（其实就是重标号）

\(Code:\)

1
2
3
4
5
6
7
8
9
10
11
12
void dfs2(int x)
{
    if(!son[x])return;
    seg[son[x]]=++cnt;rev[cnt]=son[x];//rev[x]表示序列中x的对应树上节点
    top[son[x]]=top[x];dfs2(son[x]);//直接访问son[x]保证连续性
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x]||y==son[x])continue;
        seg[y]=++cnt;rev[cnt]=y;//用seg[0]代替cnt可以省空间
        top[y]=y;dfs2(y);
    }
}

接下来的问题是：

如果要查询一条路径上的权值和/最大值，怎么办呢？

记\(x\)到\(y\)的路径权值和为\(sum(x,y)\)。

来看这张图：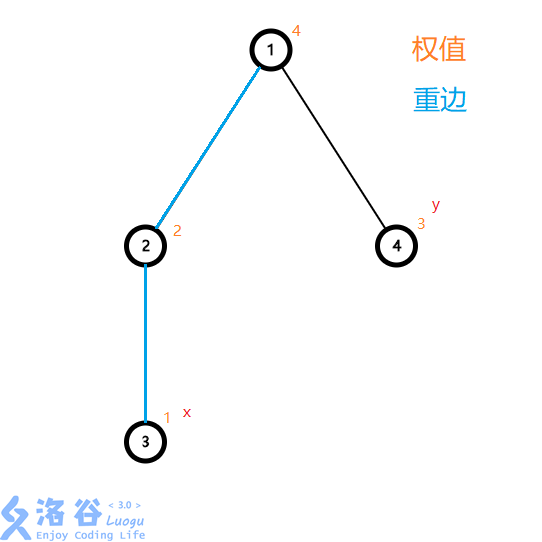

假设现在查询\(sum(3,4)\)

将上图树拆成序列，用线段树维护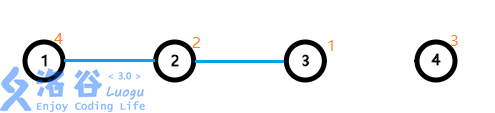

可以发现，如果\(top_x\neq top_y\)，那么\(dep_{top}\)较大的那条链的全部节点都在答案中（即\(sum(x,top_x)\in sum(x,y)\) | {\(top_x\neq top_y\ \&\ dep_x>dep_y\)}）

又因为我们的重链节点是连续储存的，在线段树中是一段区间

不用我说了吧

和之前一样，当计算完当前链的答案后，\(x\)跳到\(fa_{top_x}\)

最后\(top_x==top_y\)时，只用计算\(sum(x,y)\)这一段区间了。

整理一下：

  1. 设\(fx=top_x,fy=top_y\)。

  2. 若\(fx==fy\)，执行第4步；否则，设\(dep_x>dep_y\)，执行第三步。

  3. 计算\((x,top_x)\)对答案的贡献，\(x=fa_{top_x}\)。

  4. 设\(dep_x<dep_y\)，计算\((x,y)\)对答案的贡献

\(Code:\)（以求和为例）

1
2
3
4
5
6
7
8
9
10
11
12
13
int query_sum(int x,int y)
{
    int fx=top[x],fy=top[y],ans=0;
    while(fx!=fy)
    {
        if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
        ans+=ask_sum(1,1,n,seg[fx],seg[x]);
        x=fa[fx],fx=top[x];
    }
    if(dep[x]>dep[y])swap(x,y);
    ans+=ask_sum(1,1,n,seg[x],seg[y]);
    return ans;
}

同样的，我们可以推广到 求\(max\)/ 求\(min\) /修改 的操作

因为每次跳重链都要进行\(\Theta(lgN)\)的查询

所以时间复杂度\(\Theta(lg^2N)\)

例题P2590

认真看代码，不会很难

Code

 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include<algorithm>
#include<cstdio>
#define N 30010
using namespace std;
int head[N],ver[N<<1],next[N<<1],tot;
int dep[N],fa[N],siz[N],son[N],top[N];
int seg[N],rev[N],sum[N<<2],maxn[N<<2];
int n,m,num[N];char op[10];
inline void add(int x,int y){ver[++tot]=y;next[tot]=head[x];head[x]=tot;}
//---------------------------------------------------------
void dfs1(int x)
{
    siz[x]=1;
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x])continue;
        fa[y]=x;dep[y]=dep[x]+1;dfs1(y);
        if(siz[son[x]]<siz[y])son[x]=y;
        siz[x]+=siz[y];
    }
}
void dfs2(int x)
{
    if(!son[x])return;
    seg[son[x]]=++seg[0];rev[seg[0]]=son[x];//分配线段树节点
    top[son[x]]=top[x];dfs2(son[x]);
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x]||y==son[x])continue;
        seg[y]=++seg[0];rev[seg[0]]=y;
        top[y]=y;dfs2(y);
    }
}
//---------------------------------------------------------
void build(int p,int l,int r)//不会线段树的可以去逛我的blog
{
    if(l==r){sum[p]=maxn[p]=num[rev[l]];return;}
    int mid=l+r>>1;
    build(p<<1,l,mid);build(p<<1|1,mid+1,r);
    sum[p]=sum[p<<1]+sum[p<<1|1];
    maxn[p]=max(maxn[p<<1],maxn[p<<1|1]);
}
void change(int p,int l,int r,int x,int val)
{
    if(l==r){sum[p]=maxn[p]=val;return;}
    int mid=l+r>>1;
    if(x<=mid)change(p<<1,l,mid,x,val);
    else change(p<<1|1,mid+1,r,x,val);
    sum[p]=sum[p<<1]+sum[p<<1|1];
    maxn[p]=max(maxn[p<<1],maxn[p<<1|1]);
}
int ask_sum(int p,int l,int r,int x,int y)
{
    if(x<=l&&r<=y)return sum[p];
    int mid=l+r>>1,ans=0;
    if(x<=mid)ans=ask_sum(p<<1,l,mid,x,y);
    if(y>mid)ans+=ask_sum(p<<1|1,mid+1,r,x,y);
    return ans;
}
int ask_max(int p,int l,int r,int x,int y)
{
    if(x<=l&&r<=y)return maxn[p];
    int mid=l+r>>1,ans=-30000;
    if(x<=mid)ans=ask_max(p<<1,l,mid,x,y);
    if(y>mid)ans=max(ans,ask_max(p<<1|1,mid+1,r,x,y));
    return ans;
}
//---------------------------------------------------------
int query_max(int x,int y)//查询部分
{
    int fx=top[x],fy=top[y],ans=-30000;//记得初始化
    while(fx!=fy)
    {
        if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
        ans=max(ans,ask_max(1,1,n,seg[fx],seg[x]));//fx~x的这条链
        x=fa[fx],fx=top[x];
    }
    if(dep[x]>dep[y])swap(x,y);
    ans=max(ans,ask_max(1,1,n,seg[x],seg[y]));//x~y的这条链
    return ans;
}
int query_sum(int x,int y)
{
    int fx=top[x],fy=top[y],ans=0;
    while(fx!=fy)
    {
        if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
        ans+=ask_sum(1,1,n,seg[fx],seg[x]);//同上
        x=fa[fx],fx=top[x];
    }
    if(dep[x]>dep[y])swap(x,y);
    ans+=ask_sum(1,1,n,seg[x],seg[y]);
    return ans;
}
signed main()
{
    scanf("%d",&n);
    int x,y;
    for(int i=1;i<n;++i)
    scanf("%d%d",&x,&y),add(x,y),add(y,x);
    for(int i=1;i<=n;++i)scanf("%d",num+i);
    dep[1]=rev[1]=seg[0]=seg[1]=top[1]=1;//记得初始化！！！
    dfs1(1);dfs2(1);build(1,1,n);
    scanf("%d",&m);
    while(m--)
    {
        scanf("%s%d%d",op,&x,&y);
        if(*op=='C')change(1,1,n,seg[x],y);
        else{
            if(op[1]=='M')printf("%d\n",query_max(x,y));
            else printf("%d\n",query_sum(x,y));
        }
    }
}

后话

看完之后这些题就可以愉快地WA\(AC\)啦

  1. 【国家集训队】旅游

主要是线段树上的区间修改

解法

过程如下:

因为是区间\(*(-1)\)，所以修改后最大值是\(-(\)最小值\()\)，最小值是\(-(\)最大值\()\)，区间和是\(-(\)区间和\()\)

\(Code:\) 

1
2
3
4
5
6
void pushdown(ci&p,ci&l,ci&r)//修改节点
{
    tree[p]=Node(-tree[p].minn,//最大值 = -最小值
                 -tree[p].maxn,//最小值 = -最大值
                 -tree[p].sum,tree[p].tag^1);//区间和 = -区间和，标记 ^= 1
}
时间复杂度\(\Theta(Mlg^2N)\)

AC记录

Code 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
#include<algorithm>
#include<cstdio>
#define N 200010
#define ci const int
#define inf 0x3f3f3f3f
using std::max;
using std::min;
using std::swap;
struct Node{
    int maxn,minn,sum,tag;//区间最小，区间最大，区间和，区间标记
    Node(int _1=0,int _2=0,int _3=0,int _4=0):
        maxn(_1),minn(_2),sum(_3),tag(_4){}
    Node operator +(Node b)const
    {
        return Node(max(maxn,b.maxn),min(minn,b.minn),
                    sum+b.sum,tag|b.tag);
    }
};
Node tree[N<<2];
int head[N],ver[N<<1],next[N<<1],edge[N<<1],tot=1;//储存有向图
int fa[N],dep[N],seg[N],siz[N],son[N],top[N];//树剖必备 
int val[N],n,reb[N];char op[5];
void add(ci&x,ci&y,ci&k){ver[++tot]=y;edge[tot]=k;next[tot]=head[x];head[x]=tot;}//加条边
void dfs1(ci&x)//基本caozuo
{
    siz[x]=1;
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x])continue;
        fa[y]=x;dep[y]=dep[x]+1;//更新fa[]与dep[]
        val[y]=k;reb[k>>1]=y;//用val[x]代表x与fa[x]间的边,reb[k]表示标号为k的边在树上对应的节点
        dfs1(y);
        if(siz[son[x]]<siz[y])son[x]=y;siz[x]+=siz[y];
    }
}
void dfs2(ci&x)//同样的基本caozuo
{
    if(!son[x])return;
    seg[son[x]]=++seg[0];
    top[son[x]]=top[x];dfs2(son[x]);
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x]||y==son[x])continue;
        seg[y]=++seg[0];
        top[y]=y;dfs2(y);
    }
}
void update(ci&p)//更新节点 
{
    tree[p]=Node(max(tree[p<<1].maxn,tree[p<<1|1].maxn),
                 min(tree[p<<1].minn,tree[p<<1|1].minn),
                 tree[p<<1].sum+tree[p<<1|1].sum,tree[p].tag);
}
void pushdown(ci&p,ci&l,ci&r)//修改节点
{
    tree[p]=Node(-tree[p].minn,//最大值 = -最小值
                 -tree[p].maxn,//最小值 = -最大值
                 -tree[p].sum,tree[p].tag^1);//区间和 = -区间和，标记 ^= 1
}
void spread(ci&p,ci&l,ci&r)//标记下传
{
    if(!tree[p].tag)return;tree[p].tag=0;
    int mid=l+r>>1;
    pushdown(p<<1,l,mid);pushdown(p<<1|1,mid+1,r);
}
void change(ci&x,ci&k,ci&p=1,ci&l=1,ci&r=n)//单点修改权值
{
    if(l==r)return (void)(tree[p]=Node(k,k,k,0));
    int mid=l+r>>1;spread(p,l,r);
    if(x<=mid)change(x,k,p<<1,l,mid);
    else change(x,k,p<<1|1,mid+1,r);
    update(p);
}
void filp(ci&x,ci&y,ci&p=1,ci&l=1,ci&r=n)//区间 *= -1
{
    if(x<=l&&r<=y)return pushdown(p,l,r);
    int mid=l+r>>1;spread(p,l,r);
    if(x<=mid)filp(x,y,p<<1,l,mid);
    if(y>mid)filp(x,y,p<<1|1,mid+1,r);
    update(p);
}
Node ask(ci&x,ci&y,ci&p=1,ci&l=1,ci&r=n)//区间查询
{
    if(x<=l&&r<=y)return tree[p];
    int mid=l+r>>1;Node ans=Node(-inf,inf,0,0);spread(p,l,r);
    if(x<=mid)ans=ask(x,y,p<<1,l,mid);
    if(y>mid)ans=ans+ask(x,y,p<<1|1,mid+1,r);
    return ans;
}
void operate(int x,int y)
{
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        filp(seg[top[x]],seg[x]);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    if(x!=y)filp(seg[x]+1,seg[y]);//不能改LCA上的点
}
Node query(int x,int y)//路径查询
{
    Node ans=Node(-inf,inf,0,0);//要初始化！！！ 
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        ans=ans+ask(seg[top[x]],seg[x]);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    if(x!=y)ans=ans+ask(seg[x]+1,seg[y]);//LCA上的答案不能算~
    return ans;
}
signed main(int argc,char **argv)
{
    scanf("%d",&n);
    for(int i=1,x,y,k;i<n;++i)
        scanf("%d%d%d",&x,&y,&k),add(x+1,y+1,k),add(y+1,x+1,k);
    dep[1]=seg[0]=seg[1]=top[1]=1;
    dfs1(1);dfs2(1);
    for(int i=2;i<=n;++i)
        change(seg[i],edge[val[i]]);
    int x,y,m;
    scanf("%d\n",&m);
    while(m--)
    {
        scanf("%s%d%d",op,&x,&y);
        if(*op=='C')
            change(seg[reb[x]],y);
        else if(*op=='N')
            operate(x+1,y+1);
        else
        {
            Node ans=query(x+1,y+1);
            if(*op=='S')
                printf("%d\n",ans.sum);
            else if(op[1]=='A')
                printf("%d\n",ans.maxn);
            else printf("%d\n",ans.minn);
        }
    }
    return 0;
}

  1. 软件包管理器

解法

运用 \(dfs()\) 的性质 \(\rightarrow\) 以 \(x\) 为根的子树在线段树中为 \[[seg[x],seg[x]+siz[x]-1]\]

时间复杂度 \(\Theta(Mlg^2N)\)

AC记录

Code 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include<algorithm>
#include<cstdio>
#define N (int)1e6+10
using namespace std;
int head[N],ver[N<<1],next[N<<1],tot;
int dep[N],fa[N],siz[N],son[N],top[N];
int seg[N],rev[N],sum[N<<2];bool tag[N<<2],vis[N<<2];
int n,m;char op[10];
inline void add(const int&x,const int&y){ver[++tot]=y;next[tot]=head[x];head[x]=tot;}
//---------------------------------------------------------------
void dfs1(int x)
{
    siz[x]=1;
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x])continue;
        dep[y]=dep[x]+1;dfs1(y);
        if(siz[son[x]]<siz[y])son[x]=y;
        siz[x]+=siz[y];
    }
}
void dfs2(int x)
{
    if(!son[x])return;
    seg[son[x]]=++seg[0];top[son[x]]=top[x];
    rev[seg[0]]=son[x];dfs2(son[x]);
    for(int k=head[x],y;y=ver[k],k;k=next[k])
    {
        if(y==fa[x]||y==son[x])continue;
        seg[y]=++seg[0];top[y]=y;
        rev[seg[0]]=y;dfs2(y);
    }
}
//---------------------------------------------------------------
void spread(int p,int l,int r)
{
    if(!vis[p])return;
    int mid=l+r>>1;
    sum[p<<1]=tag[p]*(mid-l+1);sum[p<<1|1]=tag[p]*(r-mid);
    tag[p<<1]=tag[p<<1|1]=tag[p];vis[p<<1]=vis[p<<1|1]=true;vis[p]=false;
}
void change(int p,int l,int r,int x,int y,bool val)
{
    if(x<=l&&r<=y){sum[p]=val*(r-l+1);tag[p]=val;vis[p]=true;return;}
    int mid=l+r>>1;spread(p,l,r);
    if(x<=mid)change(p<<1,l,mid,x,y,val);
    if(y>mid)change(p<<1|1,mid+1,r,x,y,val);
    sum[p]=sum[p<<1]+sum[p<<1|1];
}
int ask(int p,int l,int r,int x,int y)
{
    if(x<=l&&r<=y)return sum[p];
    int mid=l+r>>1,ans=0;spread(p,l,r);
    if(x<=mid)ans+=ask(p<<1,l,mid,x,y);
    if(y>mid)ans+=ask(p<<1|1,mid+1,r,x,y);
    return ans;
}
//---------------------------------------------------------------
int install(int x)
{
    int fx=top[x],k=x,ans=0;
    while(fx!=1)
    {
        ans+=ask(1,1,seg[0],seg[fx],seg[x]);
        change(1,1,seg[0],seg[fx],seg[x],1);
        x=fa[fx],fx=top[x];
    }
    ans+=ask(1,1,seg[0],1,seg[x]);
    change(1,1,seg[0],1,seg[x],1);
    return dep[k]-ans;
}
int uninstall(int x)
{
    int ans=0;
    ans+=ask(1,1,seg[0],seg[x],seg[x]+siz[x]-1);
    change(1,1,seg[0],seg[x],seg[x]+siz[x]-1,0);
    return ans;
}
signed main()
{
    scanf("%d",&n);
    for(int i=2;i<=n;++i)
    {
        scanf("%d",fa+i);++fa[i];
        add(fa[i],i),add(i,fa[i]);
    }
    dep[1]=rev[1]=seg[0]=seg[1]=top[1]=1;
    dfs1(1);dfs2(1);
    scanf("%d",&m);int x;
    while(m--)
    {
        scanf("%s %d",op,&x);++x;
        printf("%d\n",*op=='i'?install(x):uninstall(x));
    }
}